2 Fitting occupancy models with unmarked

2.1 Occupancy Modelling with Imperfect Detection

Site occupancy surveys are frequently used in the monitoring of species. Site occupancy probabilities can be used as a metric when monitoring the current state of a population. This could be for overall changes in occupancy or the expansion/contraction of species distributions. The premise being that changes in site occupancy are correlated with changes in population size and characteristics.

However, field surveys face the problem of imperfect detection; there is no guarantee that each individual, or even each species, will be detected at a site even if it is present. The detectability of a species can be defined as the probability that at least one individual is detected in a particular sampling effort, conditional to the species being present in the area of interest during sampling. To be able to estimate the effect of imperfect detection we need to perform several independent surveys of the same site.

2.1.1 The Maths

A single species, single season occupancy model like we will cover today can be seen as a hierarchical model with two processes:

  • The state process: defined by the true site occupancy status (site occupied by the species or not)
  • The observation process: given the occupancy status, was the species detected

The true occupancy status of a site, which is unknown, is represented by the latent variable \(z_i\), which takes the value \(1\) if site \(i\) is occupied, or \(0\) otherwise, and is modelled as:

\[z_i \sim Bernoulli(\psi_i)\]

where \(\psi_i\) is the probability of occupancy. The observation process is modelled as:

\[y_{ij} | z_i \sim Bernoulli(z_i * p_{ij})\]

where \(y_{ij}\) is our detection data site \(i\) and sampling repeat \(j\), and \(p_{ij}\) is the probability of detecting the species given it is present.

As written, these equations effectively assume the probabilities of occupancy and detection are constant across all sites, when in reality sites are heterogeneous. Covariates can be incorporated into the model using a logit-link function (like in generalised linear regression), such that the occupancy and/or detectability at site \(i\) can be modelled as a function of a series of covariates \(\{x_{i1}, ..., x_{ik}\}\).

\[logit(\psi_i) = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} ... \beta_kx_{ik}\] \[logit(p_i) = \beta_0 + \beta_1x_{i1} + \beta_2x_{i2} ... \beta_kx_{ik}\]

The four main assumptions of this model are:

  • A site is closed to changes in occupancy over the survey season
  • The probability of occupancy is constant across all sites, or the variation is modelled by covariates
  • The probability of detection is constant across all sites and surveys, or the variation is modelled by covariates
  • The detection of a species and its detection histories at each site are independent

unmarked is an R package developed by Ian Fiske and Richard Chandler (and contributed to by Marc Kéry, Andy Royle, David Miller amongst others) to help users fit models accounting for the imperfect detection of unmarked individuals.

2.2 unmarked Models

unmarked is able to fit several different models under this banner. This ranges from standard occupancy models to distance sampling and colonisation extinction models. While this guide will only cover occu() for standard occupancy models, only minimal adjustment is required to fit the others

Model FittingFunction Data
Occupancy occu unmarkedFrameOccu
Royle-Nichols occuRN unmarkedFrameOccu
False Positives occuFP unmarkedFrameOccuFP
Point Count pcount unmarkedFramePCount
Generalised Point Count gpcount unmarkedFrameGPC
Open Point Count pcountOpen unmarkedFramePCO
Distance Sampling distsamp unmarkedFrameDS
Generalized Distance Sampling gdistsamp unmarkedFrameGDS
Arbitrary multinomial Poisson multinomPois unmarkedFrameMPois
Colinization Extinction colext unmarkedMultFrame
Generalized multinomial mixture gmultmix unmarkedFrameGMM

2.3 Load Package

2.4 Load Data

For this guide we will use a sample dataset supplied with the package.

site y.1 y.2 y.3 elev forest length date.1 date.2 date.3 ivel.1 ivel.2 ivel.3
1 0 0 0 -1.1729446 -1.1562281 1.8245493 -1.7614815 0.3099471 1.3813757 -0.5060353 -0.5060353 -0.5060353
2 0 0 0 -1.1265010 -0.5014837 1.6292405 -2.9043386 -1.0471958 0.5956614 -0.9336151 -0.9907486 -1.1621491
3 0 0 0 -0.1976283 -0.1013621 1.4586150 -1.6900529 -0.4757672 1.4528042 -1.1355754 -1.3388644 -1.6099164
4 0 0 0 -0.1047411 0.0077620 1.6863990 -2.1900529 -0.6900529 1.2385185 -0.8193481 -0.9272669 -1.1970640
5 0 0 0 -1.0336137 -1.1926028 1.2809338 -1.8329101 0.1670899 1.3813757 0.6375563 0.8803737 1.0422520
6 0 0 0 -0.8478392 0.9171292 1.8082888 -2.6186243 0.1670899 1.3813757 -1.3288666 -1.0422624 -0.8989603
7 0 0 0 -0.9097640 -1.0834788 1.6292405 -2.6900529 -1.1900529 1.5956614 -1.4478167 -1.5620837 -1.6763507
8 0 0 0 -1.0026513 -0.7924812 1.3083328 -2.1186243 -0.4757672 1.4528042 -0.3205880 -0.5568428 -0.6355944
9 1 1 0 -0.0582974 0.5533823 1.3350011 -2.0471958 -0.5471958 1.1670899 -0.2314744 -0.2314744 -0.0014368
10 0 0 1 -0.6311022 0.8080052 2.0412203 -2.3329101 -1.1186243 -0.2614815 -1.0968537 -1.0211703 -0.8319620
11 0 0 0 0.0655522 1.7901218 1.1314021 -1.6900529 0.4528042 1.4528042 -0.2240538 0.0579277 -0.2240538
12 0 0 0 -1.1110198 -0.6469825 1.4816045 -1.8329101 -0.3329101 1.9528042 0.4168132 0.2843674 0.5492591
13 0 0 0 -0.2595532 0.8443799 1.7917595 -0.9043386 1.0956614 1.2385185 -1.3535464 -1.0136020 -1.1592924
14 0 0 0 -0.6465834 -0.3196103 1.8245493 -2.5471958 -0.2614815 1.3099471 -1.1169952 -0.2240538 -0.7880168
15 1 0 0 0.1894019 -0.1013621 1.8082888 -1.3329101 0.3099471 1.5242328 -0.2779847 -0.1824500 0.0086195
16 1 1 0 0.1429583 1.1353774 1.5040774 -1.8329101 -1.0471958 0.5242328 -0.4826413 -0.8840994 -0.8193481
17 0 0 0 -1.2348694 0.3715089 1.8245493 -2.3329101 -0.9757672 2.3099471 -1.0699983 -1.2579860 -1.2109891
18 1 1 1 -0.9716889 -0.1377368 1.9315214 -2.4043386 -0.8329101 0.6670899 -1.1149519 -0.7348899 -0.4815152
19 0 0 0 -1.2193882 -0.9743547 1.5260563 -1.3329101 -0.2614815 1.5242328 -0.8615772 -1.1149519 -0.9882645
20 0 1 0 0.3132516 1.5718737 1.3083328 0.0242328 1.5242328 3.2385185 -0.2418364 -0.2418364 -0.3993396
21 0 0 0 -1.0026513 0.0805113 1.7404662 -1.6900529 -0.2614815 1.5956614 -0.4615119 -0.6148703 -0.4615119
22 0 0 0 0.0191086 -0.6106078 1.3862944 -1.9757672 -0.4757672 1.2385185 -0.3579950 -0.2123046 0.7346833
23 1 1 1 0.4835449 0.6988811 1.7047481 -0.4757672 0.5956614 1.6670899 0.4168132 0.6817050 0.6393223
24 0 0 0 -0.3988841 -1.0471041 1.4586150 -2.4043386 -0.9757672 0.5242328 -0.4579454 -1.5421534 -1.4337326
25 0 0 0 -0.8633204 -1.1562281 1.2237754 -2.6186243 -0.5471958 0.5242328 1.8659267 1.8830668 0.9232239
26 0 0 0 -0.9871701 -0.2832356 1.4350845 -2.7614815 -0.6186243 0.8813757 -0.2643369 0.5681799 -0.2643369
27 1 0 1 -0.5536962 0.7716305 1.6677068 -1.1900529 0.4528042 2.5956614 0.4268092 0.7016968 0.4817867
28 1 1 1 0.0655522 1.1353774 1.7227666 -0.6186243 0.5242328 2.3099471 -0.4204338 -0.2643369 -0.1082400
29 1 1 1 0.0036274 0.2987595 1.6292405 -1.0471958 0.4528042 2.0956614 0.9517906 1.4088587 1.2374582
30 0 0 0 -0.6930271 0.1896354 1.8245493 -2.1900529 -0.6186243 0.3099471 0.9038722 0.9132716 1.0542623
31 0 0 0 -0.9252452 -1.0834788 1.6486586 -2.9043386 -0.9757672 1.4528042 -1.6972264 -1.7532612 -1.5851568
32 0 0 0 -1.0645761 -1.1562281 1.7047481 -1.7614815 -0.5471958 -0.4043386 -1.0665803 -1.5433854 -1.4374287
33 0 0 0 0.1429583 0.6261317 1.7227666 -1.3329101 -0.2614815 1.3099471 -0.8366922 -0.4724661 -0.6389694
34 0 0 0 -0.3834029 0.1168860 1.4350845 -2.1186243 -0.1186243 0.5956614 0.5681799 0.1519215 0.1519215
35 0 0 0 -1.0336137 0.5170076 1.4109870 -0.7614815 -0.1900529 0.5956614 0.2229900 -0.6298321 -0.2034210
36 1 1 NA 1.0099061 -0.7197319 1.6677068 1.0956614 2.8813757 NA 0.9765844 0.0419665 NA
37 1 1 1 1.1801994 0.9898786 1.6292405 0.4528042 1.3813757 2.1670899 0.9517906 1.1231912 1.1803247
38 1 1 1 -0.1357035 1.7173724 1.2809338 -2.1186243 -0.2614815 1.5956614 0.3947389 -0.0099567 0.1519215
39 0 0 NA 1.2885679 -1.2653522 1.5475625 1.5956614 2.0956614 NA 0.3379093 0.5858931 NA
40 0 0 0 -0.6001398 -1.0834788 1.8405496 -2.1900529 -1.2614815 1.0956614 -0.7268462 -1.0968537 -1.0043518
41 1 1 1 0.8550940 0.8443799 1.2809338 -0.4757672 1.3099471 1.9528042 -0.8193481 -0.7384089 -0.9812264
42 0 0 0 -0.0892599 2.2993675 1.1939225 -1.8329101 -0.7614815 0.5956614 0.2402188 0.2402188 0.6817050
43 0 0 0 -0.8633204 -0.0649874 1.3862944 -2.3329101 -0.6186243 1.4528042 -0.1394594 -0.1394594 0.2976120
44 0 0 0 -0.9097640 0.6625064 2.1517622 -1.8329101 -0.8329101 0.5956614 -1.5082719 -1.6437979 -1.4743904
45 1 1 1 1.0253873 -0.6469825 1.9315214 0.0956614 0.6670899 1.5956614 -0.1014531 -0.2281405 -0.1014531
46 0 0 0 -0.3834029 -0.6833572 1.7749524 -1.8329101 -1.0471958 0.5956614 -0.5394907 -0.6876505 -0.7370371
47 1 1 1 -0.9871701 0.9171292 1.4586150 -1.9043386 -0.2614815 2.5956614 0.8973145 0.4907365 0.4907365
48 0 0 0 -1.1729446 -1.1926028 1.8082888 -1.8329101 -0.1186243 2.1670899 -0.3735194 -0.4690541 -0.6601236
49 1 1 1 0.3442140 0.6261317 1.7404662 -1.9757672 -0.4043386 1.5956614 -0.3081535 -0.3081535 -0.3081535
50 0 0 0 -0.4453277 0.8443799 1.9315214 -2.1186243 -0.6186243 0.5242328 -1.1994101 -0.9038063 -1.1571810
51 1 1 1 0.4371013 0.5533823 1.7749524 -2.1900529 -0.5471958 1.5242328 -0.9839701 -0.5888773 -0.8358103
52 0 0 NA 1.0408685 -0.8288559 1.5040774 -0.5471958 0.8099471 NA -0.0423324 -0.2365863 NA
53 0 0 0 0.3751764 -0.2104862 1.3083328 -2.6186243 -0.8329101 0.5956614 0.0731699 0.5456795 0.2306731
54 0 0 0 -0.8942828 -0.6833572 1.5892352 -1.6900529 -1.1900529 -0.5471958 -1.0968537 -1.2157847 -1.0373882
55 0 0 0 -0.9716889 1.7537471 1.1631508 -2.3329101 -0.2614815 0.5242328 0.3340346 0.4250911 0.7893172
56 0 0 0 -0.6620647 1.6082484 1.3862944 -2.4043386 -1.3329101 0.3813757 0.6618381 0.7346833 0.5161476
57 1 1 1 0.9479812 0.5897570 1.7404662 -0.4757672 1.0956614 1.6670899 -0.2059146 0.1008021 -0.0014368
58 0 0 0 -0.7704331 -0.9743547 1.8082888 -2.6900529 -0.7614815 0.3813757 -1.5677034 -1.5199360 -1.6154707
59 0 0 1 -0.2905156 0.3715089 1.4350845 -2.9043386 -1.0471958 0.0956614 0.5681799 0.5681799 0.5681799
60 0 0 0 -1.0181325 -1.0834788 1.8405496 -2.4043386 -1.2614815 0.4528042 -1.0968537 -1.0506028 -1.1893556
61 0 0 0 -0.6465834 1.0626280 1.5686159 -1.9757672 -0.9757672 -0.4757672 -0.3944176 -0.3944176 -0.2123046
62 0 0 0 -1.2503507 -0.7561065 2.2407097 -2.4043386 0.0956614 1.6670899 -1.2119890 -1.2739849 -1.4909707
63 0 0 NA 2.3722526 -1.2653522 0.6418539 2.6670899 3.2385185 NA 0.9187133 0.4586383 NA
64 0 0 0 -0.8168768 -1.2653522 1.6292405 -2.2614815 -0.6186243 0.1670899 -0.0194790 -0.3622800 -0.8193481
65 0 0 0 -0.8013955 -0.1741115 1.6677068 -2.3329101 -0.2614815 0.6670899 -0.1229661 0.2068991 0.7016968
66 1 1 0 -0.6930271 -0.6469825 1.9315214 -2.4043386 -0.9757672 1.0242328 -0.7348899 -0.2281405 -0.2281405
67 0 0 0 -1.1110198 1.0990027 1.5260563 -2.4043386 -0.6186243 -0.1900529 -0.6715462 -0.6715462 -0.6715462
68 0 0 0 -1.2658319 -0.1741115 1.8718022 -2.5471958 -1.1900529 0.5956614 -0.4756681 -0.6101516 -0.5204959
69 0 0 0 -1.4361252 -1.2653522 1.4350845 -1.8329101 -0.2614815 0.6670899 0.4294271 0.9844384 0.9844384
70 0 0 NA 1.1801994 -1.0834788 1.6292405 1.5956614 2.6670899 NA 0.6661231 0.6661231 NA
71 0 0 NA 1.9232975 -1.2653522 1.4109870 2.4528042 3.0242328 NA -0.4166265 -0.9851746 NA
72 0 0 1 0.2203643 1.1353774 1.7578579 -1.9043386 -0.9757672 0.8099471 -0.8026021 -0.9030782 -0.9030782
73 0 0 0 -0.6001398 -0.9743547 1.6863990 -1.9757672 -0.4757672 1.3099471 -0.1718350 -0.1718350 0.1519215
74 0 0 0 -1.0955385 1.4627496 2.1282317 -2.0471958 -0.5471958 0.5956614 -0.7846599 -0.8887245 -1.0968537
75 0 0 0 -1.1884258 1.2081268 1.9600948 -2.2614815 -0.2614815 1.5242328 -0.7919884 -0.6688697 -0.5457510
76 1 1 1 1.1801994 1.3536255 1.3862944 0.7385185 1.7385185 2.8813757 -0.7950663 -1.0136020 -0.7222211
77 1 1 1 0.6073946 2.1902434 1.6677068 -1.8329101 -0.9043386 0.1670899 0.6467193 0.5917417 0.2068991
78 1 1 1 1.0873121 0.8080052 1.7404662 -0.2614815 1.5956614 2.5956614 -0.3081535 0.3052799 -0.1036757
79 0 0 0 0.1739207 1.0626280 1.3862944 -2.1900529 0.4528042 1.4528042 0.2976120 0.2976120 0.0062311
80 1 1 1 0.2513268 0.3351342 1.5040774 -1.8329101 -0.7614815 -0.1186243 1.3821964 0.6051807 0.3461755
81 1 0 0 -0.4608089 0.3351342 1.5686159 -2.9043386 -1.1900529 -0.4757672 -0.3944176 -0.2123046 -0.3944176
82 0 0 0 -0.7239895 -0.0286127 1.9600948 -2.6900529 -1.2614815 0.3099471 -0.6688697 -0.5457510 -0.4226323
83 0 0 0 -0.8478392 -0.5014837 1.6863990 -2.4043386 -0.7614815 0.5242328 0.4756781 0.4756781 0.6375563
84 0 0 0 -1.1265010 -0.4287343 1.5686159 -1.8329101 -0.8329101 0.4528042 -0.9407568 -0.9407568 -0.9407568
85 0 NA NA 1.8304102 -1.2289775 2.1860513 0.4528042 1.5956614 NA -0.6010852 NA NA
86 1 1 1 0.7312443 0.2987595 1.6094379 -1.9043386 -0.8329101 0.5956614 0.7346833 0.5598548 0.0353692
87 1 1 1 1.3504927 -0.1741115 1.4109870 0.5242328 1.3099471 1.6670899 1.0758121 0.8626066 1.0758121
88 0 0 0 -0.6001398 -0.3196103 1.5686159 -2.4043386 -0.9757672 0.5956614 -0.2123046 0.3340346 -0.0301915
89 0 NA NA -0.6930271 -1.0107294 1.7227666 -2.9043386 -0.9043386 1.0956614 -1.5131121 NA NA
90 0 0 0 -1.0645761 1.8992459 1.8405496 -2.7614815 -1.4043386 0.0242328 -0.9581009 -1.1431046 -0.2643369
91 0 0 0 -0.5227338 0.5170076 1.5686159 -2.3329101 -0.5471958 1.3813757 0.5161476 0.7589650 0.8196694
92 0 0 0 -1.1265010 0.1532607 2.0281482 -2.1900529 -0.5471958 1.0956614 -0.6915494 -0.6148703 -0.6148703
93 1 1 1 -0.2595532 2.1174940 1.6863990 -2.4043386 -1.1900529 -0.2614815 -0.1718350 0.3677592 -0.0639162
94 0 0 0 0.4216201 0.4806329 1.5475625 -0.1900529 1.1670899 1.6670899 0.0899256 0.2139175 0.2139175
95 0 0 0 -0.5072525 -0.8652306 1.1939225 -2.2614815 -1.6900529 0.3813757 -0.7310508 -0.4661591 -0.5544564
96 1 0 1 0.0965147 1.3900002 1.8245493 -2.2614815 -0.8329101 0.1670899 0.4809000 0.1989185 0.6218907
97 0 0 0 -0.9407264 -0.8288559 1.7749524 -1.9043386 -0.9043386 1.0956614 -1.4284494 -1.1321298 -1.2802896
98 1 1 1 0.4990261 0.2623848 1.7227666 -0.2614815 1.0956614 1.7385185 -0.0041754 0.2559861 0.6722445
99 0 0 0 0.3751764 -0.3196103 1.5892352 -0.9757672 -0.4757672 0.7385185 -0.4427333 -0.2643369 0.2708525
100 0 0 0 -0.6156210 -0.7924812 1.1631508 -2.1900529 -1.1900529 0.5242328 -0.3944176 0.0608650 -0.3944176
101 0 0 0 -1.0955385 -1.1926028 1.5040774 -2.4043386 -0.9043386 -0.1186243 -0.3660889 -1.1431046 -1.2726072
102 0 0 NA 1.3969363 -0.7197319 1.4816045 1.3099471 3.2385185 NA -0.3116390 -0.0467473 NA
103 1 1 1 1.3040491 0.6988811 1.7578579 -0.7614815 1.3813757 3.1670899 0.1519215 0.1519215 -0.1997451
104 1 1 1 0.8860564 1.4263749 1.7047481 -0.2614815 0.3813757 1.5956614 0.4168132 0.7346833 -0.0070135
105 1 1 1 0.7002819 0.3715089 1.4586150 -0.4043386 0.4528042 1.5242328 0.5584995 0.9650775 0.5584995
106 0 0 0 -0.8323580 0.9535039 1.7749524 -2.3329101 -0.8329101 0.6670899 -0.1937846 -0.2925578 -0.1443980
107 0 0 0 -1.0026513 -0.0649874 1.7047481 -2.5471958 -1.6186243 0.5242328 -0.4308402 -0.1659485 -0.2189269
108 0 0 0 -0.8013955 0.6988811 1.2527630 -1.9757672 -0.5471958 0.5956614 -0.3475886 0.0353692 -0.0978335
109 1 1 1 0.2822892 1.2445015 1.2527630 -0.8329101 0.5242328 1.6670899 0.9844384 0.9844384 0.9844384
110 0 0 0 0.1739207 0.4442583 1.9459101 -1.6186243 -1.1186243 1.5956614 -1.0136020 -1.0552278 -1.0136020
111 0 0 0 -0.7859143 -1.0834788 1.8718022 -1.1900529 -0.9757672 0.0956614 -1.1480855 -1.0584298 -1.1480855
112 0 0 0 -1.0800573 0.0441367 2.0412203 -2.3329101 -0.2614815 1.0956614 -0.6049119 -0.2643369 -0.4913869
113 1 1 1 1.2730867 0.9171292 1.5686159 1.2385185 1.5956614 1.9528042 0.8803737 1.2445999 1.2445999
114 0 1 1 -0.5846586 1.3536255 1.1939225 -1.9757672 -0.1900529 0.5242328 -0.5544564 -0.0246729 0.2402188
115 0 0 0 -0.2595532 -0.2104862 1.5260563 -2.3329101 -0.5471958 1.4528042 -0.3548278 -0.4815152 -0.6082025
116 0 0 0 -0.7704331 -1.0107294 1.7227666 -1.9757672 -0.5471958 0.5956614 -0.5244984 -0.4724661 -0.8366922
117 0 0 0 -1.0645761 -1.0107294 1.4586150 -2.3329101 -0.9043386 0.6670899 0.3552105 0.6940255 1.0328405
118 0 0 0 -1.2039070 -0.7924812 1.4586150 -2.3329101 -0.9757672 0.6670899 -0.7289974 -0.7289974 -0.3224194
119 0 0 0 -1.3277567 -1.1926028 2.1162555 -2.3329101 -1.0471958 0.5956614 -1.3927482 -1.4980666 -1.2172176
120 1 1 1 0.3442140 -0.6833572 1.6863990 -0.3329101 2.6670899 2.7385185 -0.0099567 -0.0099567 0.1519215
121 0 0 0 -0.9097640 0.9898786 1.3862944 -2.3329101 -0.8329101 0.5956614 0.0062311 0.4433024 0.3704572
122 0 0 0 -1.1574634 -0.9379800 1.9600948 -1.8329101 -0.2614815 0.6670899 -0.9971862 -0.5047114 -0.4226323
123 0 0 0 -1.1884258 0.0805113 2.0014800 -2.3329101 -0.4043386 0.6670899 -1.1081039 -0.8718491 -0.9899765
124 0 0 0 -1.0336137 1.3172508 1.7404662 -2.5471958 -0.5471958 0.1670899 -0.5126314 -0.6659897 -0.6148703
125 1 1 1 1.1647182 0.2260101 1.5686159 2.1670899 3.0956614 3.5242328 1.9730521 1.7909390 1.6088260
126 1 0 NA 0.5919134 -0.5742331 1.0986123 1.8813757 3.0242328 NA 3.0657304 3.0657304 NA
127 0 0 0 -0.7394707 -0.3923596 1.9021075 -2.5471958 -1.1900529 0.8813757 -0.4134444 -0.2829753 0.1084318
128 0 0 0 -1.1419822 -0.9016053 1.8718022 -2.6900529 -0.5471958 -0.2614815 -0.8342907 -0.6549794 -0.8522218
129 0 0 0 -1.0800573 -1.2653522 1.8082888 -1.9757672 0.3099471 0.8099471 -1.3766339 -1.3766339 -1.4244013
130 0 0 0 -1.0645761 1.2808761 1.8245493 -2.6900529 -0.8329101 0.8813757 -0.6470261 0.0579277 0.2459154
131 1 1 1 1.0408685 0.3715089 1.7749524 1.0956614 1.5956614 2.0956614 -0.9839701 -0.5394907 -0.5394907
132 0 0 0 -1.0645761 -0.6106078 1.4350845 -2.7614815 -1.3329101 1.3813757 -0.6805953 -1.0274773 -0.8193481
133 0 0 0 -1.0800573 -0.5378584 1.8718022 -2.7614815 -1.0471958 0.5242328 -1.1480855 -1.1480855 -1.1480855
134 0 0 0 -1.1419822 -1.1562281 1.6094379 -2.4043386 -0.9043386 1.0956614 -1.0136020 -0.6639449 -0.6639449
135 0 0 0 -0.5536962 -0.5378584 1.8082888 -1.9757672 -0.6186243 1.3099471 0.1041542 0.1041542 0.5818278
136 0 0 0 -0.7859143 0.0441367 1.4586150 -2.2614815 -1.1900529 0.5242328 1.1683665 1.5071815 1.1006035
137 0 0 0 -0.8788016 -0.5742331 1.6863990 -2.5471958 -0.5471958 0.7385185 -1.1215209 -0.3337133 -0.1610431
138 1 0 0 0.8086503 0.0077620 1.2809338 0.5956614 1.5242328 1.6670899 0.5566172 0.3137998 0.8803737
139 0 0 0 -0.4298465 1.8992459 1.9459101 -2.6900529 -0.1900529 0.8099471 -1.0968537 -0.8887245 -0.8470986
140 1 1 1 0.1119959 0.5897570 1.7578579 -0.9043386 -0.4757672 0.5242328 -0.6518878 -0.6518878 -0.6518878
141 0 0 0 -0.4143653 -0.5014837 1.4350845 -1.1186243 -0.1186243 1.5242328 0.5681799 0.9844384 2.6494720
142 0 0 0 -0.9871701 -0.8652306 1.8082888 -2.4043386 -0.1900529 2.0242328 -0.4690541 -0.1824500 -0.1824500
143 0 0 0 -1.1265010 -0.2104862 1.5475625 -2.3329101 -0.6186243 0.8813757 -1.0879971 -0.7160215 -0.9020093
144 0 0 0 -1.0955385 0.7352558 1.5892352 -2.8329101 -0.9757672 0.7385185 -0.0859404 -0.0264749 0.5087145
145 0 1 NA 1.0873121 -0.1013621 1.9315214 0.7385185 2.1670899 NA -0.7348899 -0.4815152 NA
146 1 0 1 0.3442140 -0.1013621 1.5040774 -1.0471958 -0.4757672 1.0956614 -0.0423324 -0.0423324 0.1519215
147 0 0 0 -1.0955385 -1.1562281 1.6486586 -1.9757672 -0.5471958 0.5956614 -1.2489481 -1.4170525 -1.3610177
148 0 0 NA -0.5382150 0.8443799 1.6094379 -0.7614815 0.0956614 1.3099471 -0.3725641 -0.3142879 NA
149 0 1 1 1.1956806 0.0441367 1.4816045 1.1670899 2.1670899 3.1670899 1.0128196 1.1452655 1.2777113
150 0 0 0 0.7467255 1.8628712 1.6094379 -0.1900529 1.3099471 2.1670899 -0.0811832 -0.3725641 -0.4424955
151 0 1 1 0.0500710 1.4627496 1.5260563 -2.6900529 -0.5471958 1.4528042 0.3419525 0.2152652 0.6586709
152 1 0 0 -1.2348694 -0.4287343 1.7578579 -1.9043386 -0.6186243 0.5956614 -0.4509355 -0.5514116 -0.5514116
153 0 0 NA 1.0253873 -1.2653522 1.3350011 0.7385185 2.4528042 NA 1.2254301 1.2254301 NA
154 0 0 0 -0.3524404 1.3172508 1.9315214 -2.5471958 -0.2614815 2.1670899 -0.8615772 -0.8615772 -1.1149519
155 0 0 0 -0.4608089 1.2445015 1.9021075 -2.3329101 -1.0471958 0.6670899 -1.1962587 -0.9353206 -1.1527690
156 0 0 0 -1.0800573 -1.0471041 1.5260563 -1.8329101 -0.4757672 0.6670899 -0.4815152 -0.1014531 -0.1014531
157 0 0 0 -0.9716889 1.1717521 1.5892352 -1.7614815 -1.1186243 -0.2614815 0.8060419 0.8060419 0.8060419
158 0 0 0 -0.9716889 1.1717521 1.5892352 -1.7614815 -1.1186243 -0.2614815 0.8060419 0.8060419 0.8060419
159 0 0 0 -1.2967943 0.2623848 1.6094379 -2.4043386 -0.8329101 1.5956614 0.7346833 0.8512357 1.2008927
160 0 0 0 -0.9716889 1.3536255 1.7047481 -2.4043386 -0.8329101 1.1670899 -0.0599918 -0.0599918 0.0989432
161 0 0 0 0.2203643 1.6082484 1.3083328 -0.5471958 1.2385185 1.7385185 0.4669279 0.0731699 -0.0843332
162 0 0 0 -1.4206440 0.4442583 1.9878743 -2.7614815 -1.7614815 -0.1186243 -1.4846012 -1.2451101 -1.3249405
163 1 0 0 1.2885679 -0.3196103 1.4109870 0.9528042 2.3813757 3.8099471 1.5022232 1.5022232 1.0758121
164 0 0 0 -0.0737787 0.7716305 1.5892352 -2.3329101 -0.4043386 0.5956614 -0.2643369 -0.2643369 -0.3832678
165 1 0 NA 1.1337558 -0.6106078 1.4816045 -0.4043386 1.5956614 NA 0.6154820 0.6154820 NA
166 1 1 1 0.7002819 -0.0649874 1.0647107 0.0956614 1.5956614 3.3813757 3.0657304 3.2666827 2.9652542
167 0 0 0 0.5609510 -0.5014837 1.1939225 -0.4757672 0.5956614 1.7385185 -0.1129702 -0.3778619 -0.5544564
168 1 1 1 0.2513268 0.1532607 1.3862944 -0.5471958 -0.2614815 0.5956614 2.1187425 1.6088260 1.6088260
169 0 0 0 0.0036274 1.2445015 1.7047481 -1.6900529 -0.6186243 0.3813757 0.0989432 0.0989432 0.2578782
170 0 0 0 -0.5382150 0.2623848 1.7917595 -2.3329101 0.1670899 1.3099471 0.1519215 0.2976120 0.1033581
171 0 0 0 -0.9871701 2.2993675 1.7578579 -1.6186243 -0.2614815 0.5956614 -0.3504593 -0.6518878 -0.6016497
172 1 1 1 0.3596952 0.6261317 1.2527630 -2.1186243 -0.5471958 0.4528042 0.3184249 0.3184249 0.7346833
173 0 1 0 0.2203643 2.0083700 1.4816045 -2.1900529 -0.6186243 -0.2614815 -0.5103078 0.0856986 -0.1791931
174 1 0 1 -0.4453277 0.5533823 1.4109870 -2.2614815 -0.4757672 1.4528042 0.4361956 0.0097845 0.4361956
175 0 0 0 -0.9252452 0.6988811 1.5892352 -2.6900529 -1.6900529 -0.6186243 -0.0859404 -0.2643369 -0.4427333
176 0 0 0 -1.0490949 -0.9379800 1.6292405 -1.6186243 -1.0471958 -0.8329101 -0.3622800 -0.3622800 -0.3622800
177 1 1 1 0.0655522 0.5897570 1.6094379 -1.9043386 0.0956614 1.8813757 0.5015786 0.3850262 0.3850262
178 1 0 0 -0.7239895 0.0077620 1.6486586 -2.9043386 -0.2614815 0.4528042 0.7683042 0.6001998 1.1045129
179 0 0 0 0.9944249 0.8080052 1.3350011 0.5242328 2.1670899 2.5956614 2.7590137 1.3787884 1.8388635
180 0 0 0 -1.0181325 -0.6106078 1.7578579 -2.3329101 -1.0471958 -0.5471958 -0.4509355 -0.1997451 -0.0992689
181 1 1 NA 1.1027933 -0.8288559 1.5260563 1.5956614 3.0242328 NA 1.1020766 0.9120456 NA
182 0 0 0 0.7312443 -0.0286127 1.2237754 -0.6186243 0.6670899 2.0956614 0.0662213 -0.0194790 -0.4479803
183 0 0 0 0.3287328 1.2081268 1.4109870 -1.0471958 -0.2614815 0.4528042 1.2890177 1.2890177 1.5022232
184 0 0 0 0.3287328 1.0262533 1.5475625 -0.9757672 1.3813757 2.5956614 0.0279297 -0.9020093 -0.2820500
185 1 0 0 0.1739207 0.4806329 1.5040774 -1.8329101 -0.6186243 0.0956614 0.9936885 1.1231912 1.1231912
186 0 1 1 0.9789437 -0.0649874 1.2527630 -0.4757672 0.5242328 3.3813757 1.7337035 1.2341934 1.2341934
187 1 1 0 -0.0737787 2.0083700 1.6094379 -2.9043386 -1.0471958 0.0956614 0.4433024 0.2684739 0.5598548
188 0 0 0 -1.0800573 -0.0649874 1.7917595 -2.9043386 -1.6186243 -0.4043386 -0.1394594 0.1519215 -0.4308402
189 0 0 0 -0.2131096 0.0805113 1.3862944 -1.8329101 -0.4043386 0.6670899 0.7346833 0.7346833 0.5161476
190 0 0 0 -1.1884258 -0.9743547 1.2237754 -1.8329101 -0.2614815 1.9528042 -0.4479803 0.3233221 -0.4479803
191 1 1 1 1.3195303 0.0441367 1.5475625 -0.0471958 1.6670899 2.9528042 0.3999053 1.2678483 1.1438565
192 1 1 1 1.0873121 1.1353774 1.5260563 -0.6900529 0.8813757 1.7385185 0.6586709 0.5319836 0.2786089
193 0 0 0 -0.3524404 0.7716305 1.4109870 -1.6186243 -1.0471958 -0.4757672 1.1468807 0.5072641 1.2890177
194 0 0 0 -1.1265010 -1.2653522 1.7749524 -2.1900529 -1.1900529 0.8099471 -0.1937846 -0.0950114 0.0531484
195 0 0 0 -0.3524404 0.2260101 1.6094379 -2.9043386 -0.5471958 0.5956614 0.2101977 0.3850262 0.7346833
196 0 0 0 -0.1666659 1.0262533 2.2082744 -2.1186243 0.0242328 1.7385185 -0.7446350 -0.4884760 -0.3283766
197 0 0 NA 1.2421242 -1.2653522 1.7047481 1.7385185 2.3099471 NA -0.2719052 -0.8546670 NA
198 0 1 0 0.2668080 0.0077620 1.5475625 -1.8329101 0.0956614 1.5956614 -0.3440459 -0.2820500 -0.2820500
199 0 0 0 -0.9871701 -0.7561065 2.0149030 -1.8329101 -0.1900529 0.6670899 -0.8970497 -1.2078559 -0.9359004
200 0 0 0 -1.1729446 -1.2289775 1.9740810 -2.1900529 -0.9043386 0.5242328 -0.8193481 -1.3049829 -1.0621655
201 1 1 0 0.3751764 -0.2832356 1.3609766 -1.1186243 -0.1186243 1.3099471 1.4220433 1.4967564 1.5565268
202 0 0 NA 1.6446357 -1.2653522 1.8870696 0.6670899 1.6670899 NA -0.6427536 -0.9076453 NA
203 1 0 NA 1.2421242 -1.0471041 1.4109870 0.6670899 1.8813757 NA 2.3550453 2.3550453 NA
204 0 1 NA 1.7839666 -1.2653522 1.3350011 0.6670899 1.5956614 NA 1.3787884 0.9187133 NA
205 0 0 NA 1.3504927 -1.2289775 1.3609766 0.5956614 1.0956614 NA -0.0722176 -0.0722176 NA
206 1 1 1 0.0036274 0.8443799 1.4350845 -1.9757672 -0.9043386 0.3813757 1.1925676 1.2619440 1.3313204
207 1 0 NA 1.2885679 -0.9379800 1.4816045 1.5956614 2.5956614 NA 1.6088260 1.3439342 NA
208 1 1 NA 1.6136733 -0.7561065 1.5260563 1.6670899 2.2385185 NA -0.2914842 0.0252342 NA
209 1 1 NA 1.7530042 -1.1926028 1.4586150 2.3813757 2.8813757 NA 1.9815224 2.1848114 NA
210 1 1 1 1.5672297 -0.1741115 1.9169226 0.6670899 1.4528042 2.4528042 0.3233221 0.3233221 0.3233221
211 1 1 1 0.9170188 2.1174940 2.1400662 -0.1900529 0.5956614 1.3099471 -1.3564030 -1.0478821 -1.5278036
212 1 1 1 1.0099061 1.7173724 1.8718022 0.4528042 1.3099471 1.4528042 0.1070937 -0.1170454 0.0174380
213 1 1 1 1.0718309 1.6809977 1.8245493 0.3813757 0.5242328 1.3813757 -0.0360661 0.0579277 0.1049246
214 1 1 1 1.0253873 1.7173724 1.5260563 0.0956614 1.0242328 2.0242328 1.0387329 1.0387329 1.0387329
215 0 0 NA 1.9232975 -1.2653522 1.6677068 1.4528042 2.4528042 NA 0.4927822 0.4268092 NA
216 1 1 1 0.9944249 1.2445015 1.5475625 -0.2614815 0.8813757 1.5956614 1.2802475 0.9082719 0.7470825
217 1 1 1 1.0408685 0.6625064 1.7749524 0.8099471 1.4528042 2.9528042 0.2013081 0.2013081 0.4976277
218 0 0 NA 1.6601169 -1.2653522 1.2809338 2.0956614 3.2385185 NA 2.0944608 2.0944608 NA
219 0 0 NA 1.6601169 -1.2653522 1.4109870 0.4528042 2.8813757 NA -0.2034210 -0.2034210 NA
220 0 0 NA 1.9697411 -1.2653522 1.4586150 1.5956614 2.1670899 NA 1.7104705 1.7104705 NA
221 0 0 NA 1.8149290 -1.2653522 2.2300144 0.1670899 2.0956614 NA -0.5060353 -0.8820106 NA
222 0 0 NA 2.2793653 -1.2653522 0.6931472 2.3813757 3.4528042 NA 0.1519215 0.0062311 NA
223 0 0 NA 2.4341774 -1.2653522 1.6486586 2.3099471 2.5242328 NA 1.3286520 1.1605477 NA
224 0 0 NA 1.9697411 -1.2653522 1.7749524 2.0956614 3.0956614 NA 0.2506947 0.5470143 NA
225 0 0 NA 1.1956806 -1.2653522 1.6486586 0.5956614 1.4528042 NA -0.9127394 -0.5765307 NA
226 0 0 NA 1.5053048 -1.2653522 1.5892352 1.8099471 2.1670899 NA 0.0924560 0.0924560 NA
227 0 0 NA 1.0408685 -1.2289775 1.2527630 1.5242328 1.7385185 NA 0.7346833 -0.3475886 NA
228 0 0 NA 1.3504927 -1.2653522 1.7404662 2.3813757 3.2385185 NA -1.2283037 -0.6148703 NA
229 0 0 NA 1.0408685 -1.2653522 0.3364722 1.3813757 1.8099471 NA 5.3551516 5.9795392 NA
230 0 0 NA 1.3504927 -0.7197319 1.2237754 2.2385185 2.6670899 NA 0.0662213 0.3233221 NA
231 0 0 NA 1.5053048 -1.2653522 0.1823216 2.0956614 2.6670899 NA 5.4939044 5.4939044 NA
232 0 0 NA 1.3504927 -1.2653522 1.4816045 1.1670899 2.1670899 NA -0.3778619 0.6154820 NA
233 0 0 NA 1.1956806 -1.1926028 1.6677068 0.6670899 1.5956614 NA -0.6177638 -0.4528312 NA
234 0 0 NA 1.1956806 -1.2653522 1.6486586 1.1670899 3.1670899 NA 0.2639911 0.2639911 NA
235 0 0 NA 1.6601169 -1.2653522 1.4350845 0.6670899 2.6670899 NA -0.1255841 0.1519215 NA
236 0 0 NA 1.6601169 -1.2653522 0.9932518 1.7385185 2.8099471 NA 3.7132435 3.7132435 NA
237 0 0 NA 1.8149290 -1.2653522 1.0647107 1.8099471 3.3099471 NA 1.0562070 2.2619210 NA

Data needs to be formatted for use with a specific model fitting function, and this is accomplished with a call to an appropriate unmarkedFrame. unmarkedFrame’s are a special class of object used in this package for organising our data. These are built using R’s S4 reference class system instead of the more common S3 (like a linear model object lm). The benefit of this is a formal definition and validity checking to prevent accidentally breaking it, but the consequence is a slightly different syntax for examining it (covered later). In our case, to fit an occu() model we need to use the unmarkedFrameOccu(). This requires two data.frames and a list of data.frames:

  • y: A data.frame of presence-absence records. Rows are sites, columns are repeat visits.
    • siteCovs: A data.frame of the site-level covariates. These are things that don’t change between visits like elevation, annual rainfall, distance from roads, etc.. One column per covariate
    • obsCovs: A list of data.frames for the observation-level covariates. Each covariate is its own data.frame with rows as sites and columns as repeat visits. These are things that can change between visits. Could be environmental conditions like daily temperature or cloud cover, or methodological variables like survey method (spotlighting, pitfall traps, ink cards etc.) or an observer ID.
## unmarkedFrame Object
## 
## 237 sites
## Maximum number of observations per site: 3 
## Mean number of observations per site: 2.81 
## Sites with at least one detection: 79 
## 
## Tabulation of y observations:
##    0    1 <NA> 
##  483  182   46 
## 
## Site-level covariates:
##       elev               forest         
##  Min.   :-1.436125   Min.   :-1.265352  
##  1st Qu.:-0.940726   1st Qu.:-0.974355  
##  Median :-0.166666   Median :-0.064987  
##  Mean   : 0.007612   Mean   : 0.000088  
##  3rd Qu.: 0.994425   3rd Qu.: 0.808005  
##  Max.   : 2.434177   Max.   : 2.299367  
##      length      
##  Min.   :0.1823  
##  1st Qu.:1.4351  
##  Median :1.6094  
##  Mean   :1.5924  
##  3rd Qu.:1.7750  
##  Max.   :2.2407  
## 
## Observation-level covariates:
##       date               ivel        
##  Min.   :-2.90434   Min.   :-1.7533  
##  1st Qu.:-1.11862   1st Qu.:-0.6660  
##  Median :-0.11862   Median :-0.1395  
##  Mean   :-0.00022   Mean   : 0.0000  
##  3rd Qu.: 1.30995   3rd Qu.: 0.5493  
##  Max.   : 3.80995   Max.   : 5.9795  
##  NA's   :42         NA's   :46

2.5 Standardising Data

If you haven’t done this before creating the unmarkedFrame object the syntax for subsetting changes slightly since an unmarkedFrame is an S4 class. The first $ subset is replaced with an @

2.6 Missing Data Considerations

We have two types of data in these models: our observation data and our covariate data. These models account for missing data in the two groups differently.

  • You are allowed to have missing records in your observation data. In practice this could result from varying numbers of repeat visits to a site or the loss of data. As long as a site has at least one observation it can be used in the model. Any site that has zero observations will be removed.
  • You cannot have missing covariate data. If a site is missing the data for a site-level covariate it will be removed before model fitting. If a site is missing observation-level covariate data it will only be removed if it is missing for all observations, but the observation with missing data is removed. This is very important to consider when performing model selection so we will touch on this again later.

2.7 Fitting a Model

Fitting a model with unmarked uses a similar syntax to fitting a linear model with the lm() function. The main difference is that the way a formula is defined varies. In the case of occu() it requires a double right-hand side formula for detection and occupancy covariates in that order. Essentially ~ detection formula ~ occupancy formula.

## 
## Call:
## occu(formula = ~1 ~ 1, data = umf)
## 
## Occupancy:
##  Estimate    SE     z  P(>|z|)
##    -0.665 0.139 -4.77 1.82e-06
## 
## Detection:
##  Estimate    SE    z  P(>|z|)
##      1.32 0.174 7.61 2.82e-14
## 
## AIC: 528.987

unmarked estimates are on the link-scale (logit for occu() since it uses a logit-link), and the backTransform() function coverts them back to the original scale. You need to specify a type of state or det for occupancy or detection covariates. If you have fit a model with covariates then you need to specify values for them (i.e. what is the probability of occupancy when CovA = X and CovB = Y)

## Backtransformed linear combination(s) of Occupancy estimate(s)
## 
##  Estimate     SE LinComb (Intercept)
##      0.34 0.0313  -0.665           1
## 
## Transformation: logistic
## Backtransformed linear combination(s) of Detection estimate(s)
## 
##  Estimate     SE LinComb (Intercept)
##      0.79 0.0289    1.32           1
## 
## Transformation: logistic

Alternatively, you can define an antilogit function:

## [1] 0.3396173
## [1] 0.7891817

Now, to add some covariates. First, assuming constant detection:

## 
## Call:
## occu(formula = ~1 ~ forest + elev + length, data = umf)
## 
## Occupancy:
##             Estimate    SE      z  P(>|z|)
## (Intercept)    -1.05 0.195 -5.373 7.74e-08
## forest          1.21 0.211  5.734 9.79e-09
## elev            1.39 0.229  6.070 1.28e-09
## length          0.14 0.179  0.784 4.33e-01
## 
## Detection:
##  Estimate    SE    z  P(>|z|)
##      1.32 0.175 7.53 5.13e-14
## 
## AIC: 453.6822

And some more:

## 
## Call:
## occu(formula = ~date + ivel + forest ~ forest + elev + length, 
##     data = umf)
## 
## Occupancy:
##             Estimate    SE      z  P(>|z|)
## (Intercept)   -0.154 0.320 -0.482 6.30e-01
## forest         0.339 0.305  1.110 2.67e-01
## elev           2.328 0.416  5.591 2.26e-08
## length         0.472 0.242  1.950 5.12e-02
## 
## Detection:
##             Estimate    SE     z  P(>|z|)
## (Intercept)   0.2350 0.197 1.193 2.33e-01
## date          0.0994 0.176 0.566 5.71e-01
## ivel          0.5050 0.218 2.319 2.04e-02
## forest        1.5522 0.221 7.019 2.24e-12
## 
## AIC: 433.6014

2.8 Model Selection

2.8.1 unmarked

The is an in-built model selection method using fitList() and modSel(). You can name the models whatever you like, but the convention used here is common online (even if awkward to type out, especially for large numbers of covariates).

##                                                    nPars
## psi(forest + elev + length)p(date + ivel + forest)     8
## psi(forest + elev + length)p(.)                        5
## psi(.)p(.)                                             2
##                                                       AIC
## psi(forest + elev + length)p(date + ivel + forest) 433.60
## psi(forest + elev + length)p(.)                    453.68
## psi(.)p(.)                                         528.99
##                                                    delta
## psi(forest + elev + length)p(date + ivel + forest)  0.00
## psi(forest + elev + length)p(.)                    20.08
## psi(.)p(.)                                         95.39
##                                                      AICwt
## psi(forest + elev + length)p(date + ivel + forest) 1.0e+00
## psi(forest + elev + length)p(.)                    4.4e-05
## psi(.)p(.)                                         1.9e-21
##                                                    cumltvWt
## psi(forest + elev + length)p(date + ivel + forest)     1.00
## psi(forest + elev + length)p(.)                        1.00
## psi(.)p(.)                                             1.00

2.8.2 MuMIn

All unmarked models are compatible with the functions in the MuMIn package. For example, the dredge() and pdredge() functions perform dredge-based model selection that takes a ‘full’ or ‘global’ model and fits every possible combination of covariates and ranks them by some information criteria (AIC, BIC, etc.).

## Fixed terms are "p(Int)" and "psi(Int)"
p(Int) psi(Int) p(date) p(forest) p(ivel) psi(elev) psi(forest) psi(length) df logLik AIC delta weight
15 0.2717989 0.1371948 NA 1.5844055 0.3213761 2.5016604 NA NA 5 -210.4061 430.8122 0.0000000 2.002183e-01
47 0.2270574 0.0809094 NA 1.5670653 0.5224874 2.4738438 NA 0.5137398 6 -209.7004 431.4009 0.5886862 1.491668e-01
16 0.2030971 0.1593233 0.1664722 1.6612138 0.2948331 2.4769948 NA NA 6 -209.9298 431.8596 1.0474156 1.185933e-01
63 0.2774926 -0.1777917 NA 1.5045006 0.5309495 2.3354733 0.3610538 0.4745035 7 -208.9608 431.9217 1.1095044 1.149682e-01
31 0.3012686 -0.0227557 NA 1.5541616 0.3184063 2.3982256 0.2026555 NA 6 -210.2111 432.4221 1.6099352 8.951808e-02
48 0.1788329 0.0982908 0.1319485 1.6263881 0.4746579 2.4564416 NA 0.4893203 7 -209.4140 432.8279 2.0157310 7.307912e-02
64 0.2350160 -0.1543441 0.0994379 1.5521741 0.5050283 2.3283553 0.3389721 0.4716440 8 -208.8007 433.6014 2.7892145 4.964020e-02
32 0.2306313 0.0403105 0.1517278 1.6329933 0.2928017 2.4085725 0.1462925 NA 7 -209.8344 433.6688 2.8566108 4.799529e-02
11 0.4466097 0.0915580 NA 1.4744212 NA 2.5637670 NA NA 4 -213.0908 434.1815 3.3693343 3.714173e-02
12 0.3324200 0.1241412 0.2308726 1.5993875 NA 2.5190296 NA NA 5 -212.1499 434.2997 3.4875171 3.501056e-02
27 0.4793926 -0.1087246 NA 1.4412648 NA 2.4230182 0.2761855 NA 5 -212.6709 435.3418 4.5295744 2.079310e-02
28 0.3685889 -0.0388545 0.2095462 1.5629547 NA 2.4202416 0.2118323 NA 6 -211.9236 435.8471 5.0349557 1.615017e-02
43 0.4525069 0.0889259 NA 1.4713281 NA 2.6091039 NA 0.1634937 5 -212.9256 435.8513 5.0391041 1.611670e-02
44 0.3385965 0.1197464 0.2282498 1.5945437 NA 2.5610702 NA 0.1531902 6 -212.0063 436.0126 5.2004500 1.486758e-02
59 0.4884183 -0.1255346 NA 1.4335076 NA 2.4685178 0.2959053 0.1894972 6 -212.4510 436.9020 6.0898420 9.530405e-03
60 0.3787542 -0.0597685 0.2051483 1.5517870 NA 2.4593252 0.2348551 0.1782155 7 -211.7321 437.4643 6.6520623 7.194933e-03
25 1.3157034 -1.0496155 NA NA NA 1.3475082 1.2191191 NA 4 -222.1556 452.3113 21.4990613 4.295778e-06
26 1.2844601 -1.0522406 0.1718313 NA NA 1.3354226 1.2242119 NA 5 -221.6936 453.3873 22.5751001 2.508320e-06
29 1.2445959 -1.0455354 NA NA 0.1848135 1.3455297 1.2218243 NA 5 -221.7782 453.5564 22.7441771 2.304987e-06
57 1.3157574 -1.0456432 NA NA NA 1.3892074 1.2105149 0.1401486 5 -221.8411 453.6822 22.8700249 2.164417e-06
58 1.2839466 -1.0482557 0.1728783 NA NA 1.3776263 1.2154396 0.1409657 6 -221.3706 454.7412 23.9290310 1.274620e-06
61 1.2377919 -1.0394241 NA NA 0.1965896 1.3918236 1.2121429 0.1521085 6 -221.4105 454.8210 24.0088570 1.224748e-06
30 1.2355377 -1.0486673 0.1406246 NA 0.1412025 1.3357680 1.2252015 NA 6 -221.4910 454.9820 24.1698020 1.130051e-06
62 1.2295468 -1.0429011 0.1385517 NA 0.1531505 1.3811610 1.2158195 0.1494977 7 -221.1312 456.2624 25.4501902 5.957515e-07
24 0.2291546 -0.3662072 0.3609984 1.2961532 0.7285032 NA 0.4142468 NA 6 -240.1228 492.2456 61.4333947 9.149799e-15
8 -0.0281270 -0.0475340 0.3844998 1.6052211 0.8287601 NA NA NA 5 -241.6817 493.3634 62.5512227 5.232127e-15
56 0.2664051 -0.4019090 0.3551751 1.2641240 0.6982385 NA 0.4515160 -0.0753654 7 -240.0298 494.0595 63.2473534 3.694158e-15
23 0.3842317 -0.4417472 NA 1.1495425 0.7932479 NA 0.4703237 NA 5 -242.2418 494.4836 63.6714068 2.988363e-15
40 -0.0341475 -0.0408255 0.3867366 1.6029884 0.8404482 NA NA 0.0485674 6 -241.6422 495.2844 64.4722034 2.002362e-15
55 0.4367117 -0.4864980 NA 1.1029636 0.7444892 NA 0.5199886 -0.1109263 6 -242.0311 496.0622 65.2500407 1.357180e-15
9 1.2440471 -0.7238769 NA NA NA 0.9071172 NA NA 3 -245.2019 496.4038 65.5916172 1.144103e-15
41 1.2392010 -0.7231367 NA NA NA 0.9940344 NA 0.2375585 4 -244.2499 496.4999 65.6876733 1.090452e-15
7 0.0817147 -0.0911363 NA 1.5057697 0.9449782 NA NA NA 4 -244.3417 496.6834 65.8711944 9.948454e-16
45 1.1346845 -0.7114837 NA NA 0.2496379 1.0088969 NA 0.2674159 5 -243.6462 497.2924 66.4802152 7.336829e-16
13 1.1696647 -0.7199777 NA NA 0.2033234 0.9001801 NA NA 4 -244.8389 497.6777 66.8655382 6.051132e-16
10 1.2380311 -0.7311123 0.0959000 NA NA 0.8852939 NA NA 4 -245.0790 498.1580 67.3458410 4.759268e-16
42 1.2326285 -0.7304323 0.0995715 NA NA 0.9709839 NA 0.2350621 5 -244.1140 498.2280 67.4157894 4.595693e-16
20 0.8339574 -0.6808379 0.4001558 0.7679528 NA NA 0.6833542 NA 5 -244.1575 498.3149 67.5027332 4.400190e-16
39 0.0785087 -0.0875094 NA 1.5047510 0.9518323 NA NA 0.0269958 5 -244.3292 498.6584 67.8461669 3.705918e-16
52 0.8389858 -0.6870414 0.3882027 0.7653299 NA NA 0.7103056 -0.1974959 6 -243.3853 498.7706 67.9584442 3.503605e-16
46 1.1380968 -0.7150126 0.0360656 NA 0.2357348 0.9982608 NA 0.2636282 6 -243.6305 499.2611 68.4488704 2.741703e-16
14 1.1728537 -0.7244779 0.0552900 NA 0.1846012 0.8879189 NA NA 5 -244.8010 499.6021 68.7899069 2.311880e-16
19 1.0712302 -0.7239623 NA 0.5284574 NA NA 0.7187187 NA 4 -246.3815 500.7631 69.9508739 1.293792e-16
51 1.0614332 -0.7253322 NA 0.5431030 NA NA 0.7427912 -0.2105270 5 -245.5000 500.9999 70.1877339 1.149294e-16
17 1.3384933 -0.7556707 NA NA NA NA 0.7644613 NA 3 -248.7650 503.5299 72.7177422 3.243745e-17
18 1.2778608 -0.7514852 0.2275269 NA NA NA 0.7692585 NA 4 -247.9271 503.8542 73.0419657 2.758306e-17
49 1.3369779 -0.7601678 NA NA NA NA 0.7921068 -0.1987465 4 -247.9441 503.8883 73.0760790 2.711657e-17
50 1.2780446 -0.7569066 0.2245248 NA NA NA 0.7972470 -0.1958420 5 -247.1296 504.2592 73.4470266 2.252602e-17
21 1.2426829 -0.7478339 NA NA 0.2229338 NA 0.7667187 NA 4 -248.2337 504.4674 73.6551805 2.029946e-17
53 1.2506170 -0.7540493 NA NA 0.2082875 NA 0.7933912 -0.1905279 5 -247.4794 504.9587 74.1465435 1.587766e-17
22 1.2103185 -0.7449714 0.1969607 NA 0.1730673 NA 0.7710529 NA 5 -247.6368 505.2737 74.4614681 1.356442e-17
54 1.2194474 -0.7518920 0.1961805 NA 0.1566134 NA 0.7977083 -0.1897549 6 -246.8906 505.7812 74.9690300 1.052412e-17
4 0.2541686 -0.2009794 0.5594061 1.5617529 NA NA NA NA 4 -249.8103 507.6206 76.8084088 4.195364e-18
36 0.2357155 -0.1708860 0.5396890 1.5978246 NA NA NA -0.2291602 5 -249.1665 508.3329 77.5207357 2.938257e-18
3 0.5617480 -0.3685693 NA 1.2354923 NA NA NA NA 3 -255.5722 517.1444 86.3322160 3.586751e-20
35 0.5167888 -0.3205897 NA 1.3043660 NA NA NA -0.2659546 4 -254.6159 517.2317 86.4195251 3.433541e-20
1 1.3249166 -0.6650338 NA NA NA NA NA NA 2 -262.4935 528.9870 98.1747779 9.618815e-23
2 1.2749717 -0.6639879 0.2096239 NA NA NA NA NA 3 -261.7925 529.5850 98.7728449 7.132684e-23
5 1.2234967 -0.6563222 NA NA 0.2367346 NA NA NA 3 -261.9381 529.8763 99.0640771 6.166130e-23
33 1.3236477 -0.6656290 NA NA NA NA NA -0.0878263 3 -262.2988 530.5975 99.7853108 4.299310e-23
6 1.2000292 -0.6562906 0.1768538 NA 0.1903936 NA NA NA 4 -261.4647 530.9294 100.1171656 3.641979e-23
34 1.2752897 -0.6649410 0.2066496 NA NA NA NA -0.0821538 4 -261.6203 531.2406 100.4284182 3.117093e-23
37 1.2280744 -0.6582929 NA NA 0.2282182 NA NA -0.0761202 4 -261.7907 531.5814 100.7691800 2.628780e-23
38 1.2051423 -0.6582980 0.1756097 NA 0.1817536 NA NA -0.0738349 5 -261.3252 532.6504 101.8381625 1.540379e-23

2.8.3 Missing Data

As mentioned previously, missing data can have serious impacts on model selection. This is because information criterion like AIC are not comparable between models fit to different datasets. If you fit Model A with covariates 1 & 2 with 100 sites, and Model B with covariates 1, 2, & 3 with 90 sites (because covariate 3 is missing data) then you cannot compare AIC. This rule holds no matter how minuscule the difference is (e.g. 10,000 vs 9,999).

To account for this you need to manually remove the data for all sites/observations that are missing data for any covariates that could potentially be included in your model. In the previous example, both Model A and Model B should be fit to the 90 sites not missing data for covariate 3.

2.9 Proportion of Area Occupied

Imperfect detection can bias our occupancy estimates. So how do we calculate the actual proportion of area occupied by our target species while accounting for imperfect detection?

2.9.1 Assuming perfect detection

If we naively assumed perfect detection the proportion of area occupied by a species is simply the proportion of occupied sites: number of sites where the species was observed divided by the total number of sites.

## [1] 0.3333333

2.9.2 Accounting for Imperfect Detection

In reality we wouldn’t assume perfect detection, so we need to account for it otherwise we will end up with a biased underestimate of the proportion of area occupied. unmarked utilises empirical Bayes methods to estimate the posterior distributions of the random variables (here, latent occurrence state, \(z_i\)).

\[Pr(z_i = 1 | y_{ij}, \psi_i, p_{ij})\]

##      Estimate        5%       95%
## PAO 0.4858397 0.4219409 0.5949367

A difference in the proportion of area occupied of over 15%! Depending on how hard a species can be to detect with a given survey method this difference can potentially be much higher!

2.10 Prediction

Lets load in a bigger dataset for this one. This is a dataset for ink card surveys for the giant gecko, Cyrtodactylus sadleiri, on Christmas Island.

Now lets fit a model with a larger amount of covariates. We can also alter some additional model parameters. method sets to optimisation method used by optim under the hood to estimate the maximum likelihood, control here sets the maximum number of iterations allowed for the model to converge (the default value is rather small so this is useful for more complex models), and engine gives you the choice to run the optimisation in native R code or fast C++.

## Warning: Some observations have been discarded
## because corresponding covariates were missing.
## Warning: 100 sites have been discarded because of
## missing data.

Now we load in the data we want to predict occupancy for. This dataset needs to have two columns for longitude and latitude values for each site/pixel, and a column for each covariate (each row is one site/pixel). Categorical variables need to have a single level specified per site. This is straight forward for something like vegetation class, but for methodological variables like survey method(ink cards, spotlighting, etc.) you need to select one a priori.

And predict.

##   doing row 1000 of 27593 
##   doing row 2000 of 27593 
##   doing row 3000 of 27593 
##   doing row 4000 of 27593 
##   doing row 5000 of 27593 
##   doing row 6000 of 27593 
##   doing row 7000 of 27593 
##   doing row 8000 of 27593 
##   doing row 9000 of 27593 
##   doing row 10000 of 27593 
##   doing row 11000 of 27593 
##   doing row 12000 of 27593 
##   doing row 13000 of 27593 
##   doing row 14000 of 27593 
##   doing row 15000 of 27593 
##   doing row 16000 of 27593 
##   doing row 17000 of 27593 
##   doing row 18000 of 27593 
##   doing row 19000 of 27593 
##   doing row 20000 of 27593 
##   doing row 21000 of 27593 
##   doing row 22000 of 27593 
##   doing row 23000 of 27593 
##   doing row 24000 of 27593 
##   doing row 25000 of 27593 
##   doing row 26000 of 27593 
##   doing row 27000 of 27593

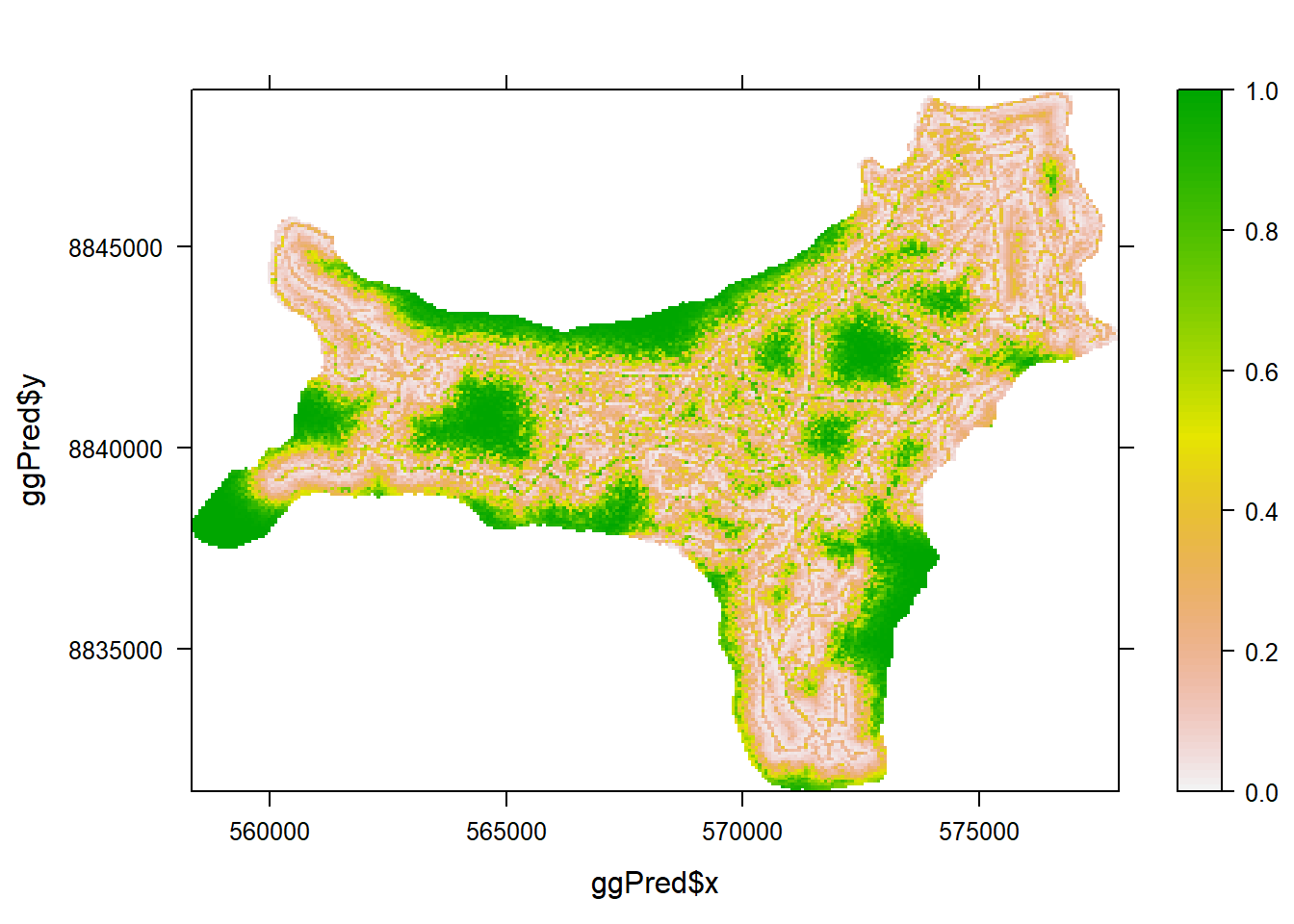
2.11 Model Evaluation

A vital step in modelling is evaluating the accuracy of model predictions. Model evaluation usually involves testing how well our model can predict data not used in the model fitting process. Does our model predict high probability of occupancy for sites with observed presences in our hold-out data? Does it predict low probability of ocurrence for the sites with observed absences? The Area Under the Receiver Operating Curve (AUC) is a popular metric for this evaluation.

The problem with this type of model evaluation for models accounting for imperfect detection is that we don’t know the true occupancy state of a site. Is the species actually absent from the site in our hold-out data, or did we just fail to detect it? As such this type of model evaluation is not appropriate for our modelling method.

Instead we can use several goodness-of-fit tests to perform model evaluation. Here we use three tests: sum of squared errors, Pearson’s Chi-squared, and Freeman-Tukey Chi-squared. We create a new function called fitstats (where model.name should be replaced with your own), and then use it when fitting our model to bootsrapped samples of our data to assess model fit. Even though these are called goodness-of-fit tests they are looking for significant lack-of-fit evidence (which sounds too pessimistic), so a p-value of <0.05 is actually a poorly fit model. A “good” model should return a value >> 0.05 for each test. Yet the issue of imperfect detection can still impact these tests. It is possible to fail one test but pass the others on the basis of poor prediction at a small subset of sites (even one). For example, an observed presence at a really low probability of detection site can dramatically inflate the test statistic. In these scenarios it is important to assess the input of each site to the test statistic to determine if the “lack-of-fit” can be disregarded as over-penalising the mismatch in a very low proportion of sites.

2.12 Common Errors

  • Error: Hessian is singular. Try providing starting values or using fewer covariates. (The bane of my Masters existence)
    • This could come about for a variety of reasons.
    • For models with a very low naive occupancy rate, especially in small datasets, you might need to specify starting values for the maximum likelihood estimation (see ?occu)
    • You have complete separation in one or more covariates. This means the model doesn’t have the necessary data to calculate parameter estimates. For categorical variables this is commonly a factor level that has exclusively presence or absence observations (or potentially when the prevalence is near 0 or 1 in very big datasets), or there are factor levels in two or more categorical variables that never co-occur. Consider merging factor levels if possible! For continuous variables this is where the data is split into two (or more) groups at either end of a sampling range. For example, you are including elevation as a covariate but have presence records only at 0-20m, and absences only at 80-100m. The model then can’t estimate the slope of the relationship.
    • You have somehow got a continuous variable set to factor
    • You have too many covariates in the model for your data. There is no set rule for this and different people will give different answers. Every 10 sites allows one covariate, every 10 presences allows one covariate, every 10 allows one covariate in each formula, each level in a categorical variable is treated as a separate binary dummy variable and it does/does not count as a separate covariate for this count etc..
  • Something about factor levels and prediction.
    • If you have a model with a categorical covariate with 5 factor levels, the data being predicted to must have 5 levels. Each site being predicted to can have the same level, but the data must be allowed to have other levels. This is an R error and not a statistical error. This is commonly caused by methodological observation-level covariates. For example, your data comes from three different survey methods (e.g. spotlighting, trapping, and drones), you fit the model and find out that spotlighting has the best probability of detecting your target species, and then predict to only spotlighting as a survey method. A really easy mistake to make!
    • A dodgy fix: Set a random cell on the border of the area you are predicting to to the missing factor level
    • A proper fix: Use the levels() function to set additional levels to your prediction data
  • Your fitted model has unrealistic parameter estimates.
    • occu() is on the logit-scale, so anything outside [-5, 5] is when you need to start checking. When this is back transformed to the probability scale it is roughly [0, 1]. There is leeway if you are considering polynomial terms. If you start getting parameter estimates of +30, -90, or +462.10 (David’s high score) then you definitely have an issue! This is equally likely to happen to categorical or continuous data.
    • This could be one of two issues:
      • Your model has not converged on the maximum likelihood. Use the control argument when fitting the model to increase the number of iterations in the optimisation process. The default is rather small at 100 or 500 depending on your optimisation method. Setting it high (i.e. 10,000) is fine, as it is a maximum, and the model will stop if it converges earlier.
      • Your model has converged on a local maximum. Likelihoods can have multiple peaks, but only one maximum, and your model is stuck on the wrong one. To fix this use the starts argument to provide starting values for parameters to start the optimisation in a different area.
  • Model selection with dredge() is too much for my computer to handle. + See David (for Spartan) or Casey/Nick (for Boab)

2.13 Additional resources